Qu’est ce que l’information ?
Voilà une question bien plus profonde qu’il n’y paraît. De nos jours, cette notion d’information semble triviale. On entend ce terme relativement souvent, et sa compréhension paraît intuitive, bien qu’elle recouvre différents sens [1]. Pour autant, si l’on demande au profane sa définition, il vous répondra sûrement que les informations ont lieu vers 13h et 20h tous les jours à la télé, ou toutes les heures à la radio ; ou encore tous les jours via la presse. Chacun a une idée générale de ce qu’elle représente, sans pour autant expliciter une définition. Dans le domaine militaire ou policier, information rime avec espionnage ou enquête et la dure acquisition de renseignements concernant l’ennemi, tout en travaillant à ne pas lui dévoiler ceux nous concernant. D’autres personnes plus folles vous parleront de théorie des jeux, de probabilités, d’économie, de psychologie humaine.

Certains, encore plus fous, vous parleront même de physique quantique, ou de thermodynamique des trous noirs (nous y reviendrons d’ailleurs dans un prochain article).
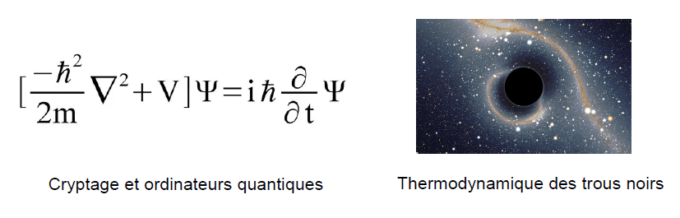
Et pourtant, dans leur acceptation quotidienne de la notion d’information, ils ont tous quelque part raison, sans pour que celle-ci ne repose sur une définition commune. Là où le mystère devient encore plus intrigant, c’est qu’il n’existe pas de définition précise et faisant consensus du concept «information». Ou plutôt, de multiples définitions subsistent, et se côtoient, selon les disciplines.
La nécessité de définir un concept
Sans retracer l’histoire de ce concept dans son ensemble, le terme information vient du latin informare (donner forme à) [2]. Il s’agit d’une traduction relative à plusieurs notions grecques, qui désignent la forme visuelle εἶδος, eidos (racine indo-européenne *weid– qui donnera, entre autres, video [3] et εἴδησις, eídêsis dont je me suis inspiré pour le nom du site) ; l’apparence, l’aspect ἰδέᾱ, idea (de la même racine *weid– [3]) ; ou la forme, la structure μορφή, morphé [2]. La notion d’information ne semble alors pas avoir de définition bien précise. Elle renvoie à la faculté de modeler, de donner forme, d’instruire. Le professeur instruit ses élèves et donne forme à leurs connaissances, leur expérience, leur personnalité. Une seconde conception de l’information renvoie au fait de transmettre et communiquer quelque chose à quelqu’un.
Les conceptions modernes de l’information sont nombreuses, vagues, parfois mystiques ou ésotériques. Chacun semble avoir sa définition, que ce soit selon son domaine de travail ou ses croyances, et cela mériterait un exposé en soi. Il est important de noter que le besoin de bien définir ce concept s’éprouve dans de nombreuses disciplines [2][4][5] :
- en sciences, avec la biologie et la physique
- en télécommunications
- dans le contrôle des systèmes, la cybernétique
- en sciences humaines et sociales
- en philosophie
- en sciences de l’information, discipline large et floue (peu connue en France), qui s’attache à étudier l’archivage, l’analyse de l’information selon des critères précis.
Même si l’idée générale que l’on a de l’information se révèle suffisante dans notre vie quotidienne, elle reste imprécise et peut même porter à confusion dans des domaines plus techniques où elle est utilisée, notamment en sciences. De fait, pour bien appréhender ce concept, il est nécessaire de disposer d’une définition précise, universelle, qui nous permette également de saisir les règles, les propriétés qui encadrent cette notion. En l’occurrence, toutes les tentatives récentes de parvenir à une définition bien établie reposent un socle de départ commun.
Une théorie mathématique des communications

Claude Elwood Shannon (1916 – 2001) est un ingénieur en génie électronique. Il fait ses études au MIT de 1936 à 1940 où il travaille avec passion sur l’algèbre de Boole et ses applications en électronique. En 1941, il rejoint une autre prestigieuse université américaine, Princeton. Il y côtoie de fameuses personnalités comme Albert Einstein, Kurt Gödel, John von Neumann et travaille avec John Robinson Pierce [Note 1]. C’est dans ce contexte, entouré de personnalités diverses et enrichissantes que Shannon commence à saisir les subtilités concernant la communication d’une information. Durant la guerre, il intègre les Bell Labs et travaille dans un service de chiffrement, où il rencontre brièvement Alan Turing. Son intérêt réside surtout dans la problématique de « séparation du signal par rapport au bruit » dans les télécommunications [6]. Après la guerre, Shannon publie sa théorie « A Mathematical Theory of Communications » en 1948 [7]. Elle s’appuie largement sur les travaux de Harry Nyquist et Ralph Hartley, deux chercheurs en ingénierie électronique [Note 2]. Preuve en est de l’expertise qui règne alors dans la recherche américaine en télécommunications, le transistor est dévoilé la même année et dans le même centre de recherche [Notes 1b et 2b].
Le succès de la théorie de l’information
En parallèle, Norbert Wiener publie son expérience acquise au cours de la guerre dans le contrôle des systèmes automatiques « Cybernetics : Or control and communication in the animal and the machine » [8]. Cybernétique et théorie de l’information sont les deux facettes d’une même pièce, abordant le sujet de l’information selon deux approches différentes, mais complémentaires [Note 3]. La théorie de l’information de Shannon se concentre sur la communication pure, les processus de distinction entre signal et bruit et la façon optimale de transmettre de l’information. La cybernétique s’applique à comprendre comment contrôler cette information, et comment appliquer ce contrôle pour améliorer les systèmes. Ces deux domaines vont connaître un essor considérable, en partie grâce aux conférences Macy, qui regroupent des chercheurs de plusieurs disciplines, et vont en étendre les possibilités d’application. Ces conférences verront se rencontrer une pléthore de noms célèbres, et serviront d’incubateur à idées et à rencontres interdisciplinaires, influençant profondément de nombreux champs de recherche comme la robotique, l’intelligence artificielle, la physiologie, la neurobiologie, l’éthologie ou encore la linguistique.
La rançon du succès
Dans le cadre de ce travail, nous suivrons rigoureusement la définition mathématique publiée par Shannon [7]. Il fut le modeste père d’un champ d’application considérable et bien trop méconnu que l’on nomme la théorie de l’information. Son travail n’a pas seulement permis d’améliorer les transmissions à distance, il a aussi servi de base au développement de toutes les télécommunications modernes, des méthodes de compression des données, du développement de nouveaux procédés comme les codes correcteurs d’erreurs. Il serait difficile de cerner précisément à quel point son travail, d’apparence simple, a pu influer sur la révolution numérique que nous connaissons.
Comme je l’expliquais plus haut, déjà à l’époque, son travail connut un retentissement considérable. Cependant, l’extension de sa théorie à des domaines autres que les télécommunications fut si rapide et hors de proportion, que cela souleva des questionnements sur les applications de ces idées. De nature plutôt modeste et perfectionniste, Shannon craignit une application irraisonnée de son travail. Il s’appliquera à freiner toutes ces ardeurs en publiant 8 ans plus tard, en 1956, un court article expliquant son souhait [9].
Cette intervention laisse alors la théorie de l’information dans l’ unique champ de l’ingénierie des communications, l’écartant des autres domaines de recherche. Néanmoins, son travail resurgit dans les années 1990, avec des applications plus rigoureuses en biologie moléculaire [10] et évolutive [11][12], et tend à revenir dans la lumière scientifique générale.
Dans le prochain article, nous reviendrons sur cet article fondateur publié par Shannon. Nous nous pencherons sur son contenu, les idées novatrices qu’il apporte, mais aussi, nous reviendrons sur les quelques imprécisions et ambiguïtés qui sont, encore aujourd’hui, à l’origine de nombreuses mauvaises interprétations de la notion d’information.
Source
[1] http://www.cnrtl.fr/definition/information
[2] Capurro, R., & Hjørland, B. ; « The concept of information » in Annual Review of Information Science and Technology Ed. B. Cronin, Vol. 37 (2003) Chapter 8, pp. 343-411.
[3] Jean-Claude Rolland (2016) ; Les grandes familles de mots, 3ème édition ; Rolland
[4] Bates, Marcia J. (2010). “Information.” In Encyclopedia of Library and Information Sciences, 3rd Ed. Bates, Marcia J.; Maack, Mary Niles,Eds. New York: CRC Press, vol. 3, pp. 2347-2360.
[5] Dodig-Crnkovic, G. and Burgin, M. (2011) ; Information and Computation: Essays on Scientific and Philosophical Understanding of Foundations of Information and Computation. World Scientific Publishing Co Pte Ltd, London, pp. 7-32.
Note 1 : Il est crédité, avec Shannon et Oliver, pour avoir développé sur le PCM (Pulse Code Modulation), un procédé de représentation d’un signal numérisé, très utilisé dans les formats audio. B. M. Oliver; J. R. Pierce & C. E. Shannon (Nov 1948). « The Philosophy of PCM ». Proceedings of the IRE. 36 (11): 1324–1331. doi:10.1109/JRPROC.1948.231941. ISSN 0096-8390.
Note 1b : A titre anecdotique, J.R. Pierce est celui qui inventa le nom de transistor.
[6] Jeremy Campbell (1982) ; Grammatical Man, Information, entropy, language and life ; Simon & Schuster Inc.
Note 2 : Leurs idées et les applications qui en découlent vont grandement contribuer à l’optimisation des télécommunications. Ces travaux sont cités par Shannon dès les premières lignes de son article (voir référence [7]) :
- Nyquist (1889 – 1976) a travaillé sur les questions de bruit thermique (facteur physique perturbant les communications) et les critères d’échantillonnage (connu sous le nom de Nyquist-Shannon sampling theorem).
- Hartley (1888 – 1970) publie en 1928 un papier intitulé » Transmission de l’information » qui sera le pivot central de la réflexion de Shannon.
Note 2b : Nyquist et Hartley travaillèrent tous les deux aux Bell Labs (anciennement AT&T Bell Laboratories) ; le premier de 1917 à 1954, le second entre 1929 et 1950.
[8] Norbert Wiener (1948) ; Cybernetics: Or Control and Communication in the Animal and the Machine. Paris, (Hermann & Cie) & Camb. Mass. (MIT Press) ISBN 978-0-262-73009-9;, 2nd revised ed. 1961.
NOTE 3 : Une troisième partie du champ de l’information existe : la théorie algorithmique de l’information (AIT). Celle-ci aborde l’information dans l’aspect computationnel et algorithmique. Ce sous-champ de la théorie de l’information fut développé indépendamment par deux mathématiciens, dans les années 1960 : Gregory Chatin et le fameux statisticien Andrey Kolmogorov. Il s’agit d’un domaine un peu plus abstrait et distant, qui mélange la théorie de l’information de Shannon, et le travail sur le calcul informatique de Turing.
[9] Shannon, C.E. (1956) ; « The bandwagon », IRE Trans. Inf. Theory, vol. 2, pp. 3-3
[10] Schneider, T.D. & Stephens, R.M. (1990) ; Sequence Logos: A new way to display consensus sequences. Nucleic Acids Res. 18(20):6097-100
[11] Adami, C. & Brown, C.T. (1994) ; Evolutionary Learning in the 2D Articial Life System »Avida ». Proc. of Artificial Life IV. R. Brooks and P. Maes, eds., MIT Press pp. 377-381.
[12] Farnsworth, K.D. et al., (2013) ; Living is Information Processing: From Molecules to Global Systems. Acta Biotheor 61:203–222